分類問題に有効！マンホイットニーU検定による特徴量選択

本記事では、連続値を取る説明変数のうちどの説明変数が特徴として有効であるか知りたい場合に有用なマンホイットニーのU検定、通称「U検定」について説明します。

論よりコード、まずはPythonコードはこちら。

Pythonコード

from scipy import stats
import pandas as pd

# カラムとp値を保持
feature_list = pd.DataFrame()

# カラム１つごとに確認
for col in df1.columns:
  # ２つの連続値を比べる
  statistics, pvalue = stats.mannwhitneyu(df1[col], df2[col])
  # 例：) MannwhitneyuResult(statistic=49.0, pvalue=4.8490227224570924e-17)

  # p値とカラム名をリストに保存
  feature_list = feature_list.append(pd.DataFrame({'column':col, 'value':pvalue}, index=[len(feature_list)]))

# p値が小さいものから表示（小さいものほど度合いが高い）
print(feature_list.sort_values('value'))

U検定とは

マン－ホイットニーのＵ検定
独立した２組の標本が属している母集団の分布が等しいかどうかを検定するノンパラメトリック手法。

http://www2.hak.hokkyodai.ac.jp/fukuda/lecture/SocialLinguistics/html/12nonpara.html

つまり、正規分布しないと思われる２つの分布に対して差があるかどうかを測るものであり、p値が小さいほど「2 群の母代表値に差がある」と言えます。

これを用いて一定のp値以下のものを特徴量として取捨選択すると、結果、効率的に特徴量を選択することができます。

Irisデータによるサンプル

ここからはirisデータを使ってp値とそのデータを可視化したものを確認します。

なお今回２値分類として話を進めるため、比較する品種をvirginicaとversicolorに絞ります。

import seaborn as sns
from scipy import stats
import numpy as np
import pandas as pd

# seabornのirisデータセットを読み込み
iris = sns.load_dataset('iris') 

# カラムとp値を保持
feature_list = pd.DataFrame()

# カラム１つごとに確認
for col in iris.columns:
  # virginicaとversicolorの各カラムの分布の差を調べる（U検定）
  statistics, pvalue = stats.mannwhitneyu(iris[iris['species'] == 'virginica'][col], iris[iris['species'] == 'versicolor'][col])

  # p値とカラム名をリストに保存
  feature_list = feature_list.append(pd.DataFrame({'column':col, 'pvalue':pvalue}, index=[len(feature_list)]))

# p値が小さいものから表示（小さいものほど度合いが高い）
print(feature_list.sort_values('pvalue', ascending=False))

feature_listに入った結果は以下のようになりました。

	column	        value
2	petal_length	4.566772e-17
3	petal_width	4.849023e-17
0	sepal_length	2.934503e-07
1	sepal_width	2.286071e-03

petal_lengthという属性値が一番p値が小さくなり、sepal_widthという属性値が一番p値が大きくなりました。

では、ヒストグラムとして書き出してみるとこの違いはどう見えるでしょうか。

petal_lengthの場合

p値も十分に小さいことから、差があると言える状態でしたが、可視化してみるとかなり差があるように見受けられます（重複する部分も大分小さい）。分類に有効な特徴として使えそうですね。

では、一番大きかったsepal_widthはどうでしょうか。

sepal_widthの場合

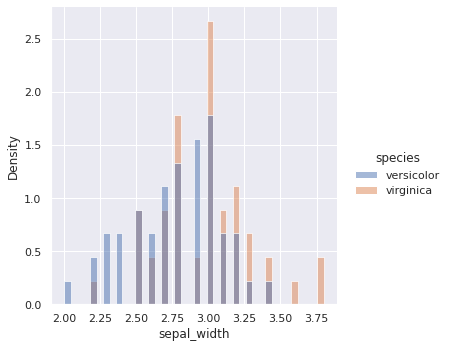
p値が0.0022〜ということでよく使われる0.05よりも小さいことから差があると言えますが、先ほどのpetal_lengthの方と比べて大分大きいことからもわかるように、あまり差があるようには見えません。重なっている部分も多いですね。

こういった説明変数を特徴として使ってもあまり精度に寄与しないでしょう。

場合によっては使わない方が精度が出る場合もあります。

まとめ

U検定による分類問題に有効な特徴量の選択に関してお話しさせていただきました。

U検定はノンパラメトリック（正規分布していないと思われる分布に使える/していてもそれほど変わらない結果が得られる）手法です。正規分布するとわかっている場合はt検定が相応しいです。

ところで、分布が正規分布しているかしていないかはどのように調べれば良いでしょうか？

その方法は今後当ブログの記事で紹介したいと思います。

それでは！